In Two Years I Will Be Twice As Old
In Two Years I Know I Ll Be Twice As Old As Five Years Ago Said Tom Riddle Answer Brainzilla
In two years i will be twice as old. Since we are given that in 2 years i will be twice as old as i was 20 years ago. In 2 years i will be twice as old as i was 20 years ago how old am i. Answer 1 of 12.
In two years I know Ill be twice as old as five years ago said Tom. In 2 years Becky will be twice as old as Joey. How can the correlation.
After two years i will be x2 years. Lots of people have landed on our website looking for the answer of this riddle. Garima went for a morning walk and met her old friend Shamita and her - 224071.
In 2 years time Jennie will be 14 years old. Our baby sister is 2 years younger than he is. Click to show spoiler.
Let x Toms age today x 2 2x - 5 x 2 2x - 10 12 x. A 10 2 B 10. X22 x-5 x2 2x-10.
Garima went for a morning walk and met her old friend Shamita and her daughter Jaya after a long time. Answer by josmiceli 19441 Show Source. X 2 2 x 5 Solvingo for x gives 12.
From 2 -- A 3B - 15 5 3B - 10. Hence i am.
In Two Years I Know I Ll Be Twice As Old As Five Years Ago Said Tom Riddle Answer Brainzilla
In Two Years I Know I Ll Be Twice As Old As Five Years Ago Said Tom How Old Is Tom Riddles Net
If Someone Says In 2 Years I Will Be Twice As Old As I Was 5 Years Ago How Old Are They Now Doyouremember
In Two Years I Know I Ll Be Twice As Old As Five Years Ago Said Tom Riddle Answer Brainzilla
In 2 Years I Will Be Twice The Age I Had 5 Years Ago What Is My Age Quora
In 10 Years A Will Be Twice As Old As B Was 10 Years Ago If A Is Now 9 Years Older Than B What Is The Present Age Of B Quora
Day 1 Brainteaser Wod A 30 Year Old Man Married A 25 Year Old Woman She Died At Age 50 And Her Husband Was So Devastated That He Cried For Years Ppt Download
When Asked How Old She Was Suzie Replied In Two
Ten Years Later A Will Be Twice As Old As B And Five Years Ago Q 2 Exercise 3 9 Rd Class 10 Youtube
In 10 Years A Will Be Twice As Old As B Was 10 Years Ago If At Present A Is 9 Years Older Than B Then Present Age Of B Is
In Lo Years A Will Be Twice As Old As B Was 10 Years Ago Scholr
Five Years Ago Nuri Was Thrice As Old As Sonu Ten Years Video
Ten Years Later A Will Be Twice As Old As B And Five Years Ago Q 2 Exercise 3 9 Rd Class 10 Youtube
Five Years Ago Lucky Would Be Thrice As Old As Lovely 10 Years Later Lucky Will Be Twiceas Old As Lovely How Old Are They Now
Five Years Ago Nuri Was Thrice As Old As Sonu Ten Years Video
Joey Is 20 Years Younger Than Becky In Two Years Gauthmath
Homework Question In Two Years Time John Will Be 3 Times As Old As He Was 10 Years Ago How Old Is John Quora
A Is Two Years Older Than B Who Is Twice As Old As C Total Of Ages Of A B And C Is 27 How Old Is B Youtube
Two Years Ago Father Was 3 Times As Old As His Son And Two Years Hence Twice His Age Will Be Eq Youtube
In Two Years I Know I Ll Be Twice As Old As Five Years Ago Said Tom How Old Is Tom Logic Lovely
6 Mary Is Twice Older Than Her Sister In 5 Years Time She Will Be 2 Years Older Than Ntr Sister Find How Old Are They Both Now In 5 Years Time
Ahmad Is 7 Years Older Than John Four Years Ago Ahmad Was Twice As Old As John Find The Sum Of Their Ages In 7 Years Time
Five Years Ago A Was Thrice As Old As B And Ten Years Later A Shall Be Twice As Old As B What Is The Present Age Of A A 20b 50c 60d 40correct Answer Is Option
How
A Is Two Years Older Than B Who Is Twice As Old As C If The Total Of The Ages Of A B And C Be 27 Then How Old Is B
Q19a Man Is Thrice As Old As H Lido
Two Years Ago Father Was 3 Times As Old As His Son And Two Years Hence Twice His Age Will Be Equal To Five Times That Of His Son S Age Find Their Present Ages
A Woman Is Twice As Old As Her Daughter Twenty Years Ago She Was Four Times As Old As Her Daughter How Old Are They Now Quora
Ten Years Later A Will Be Twice As Old As B And Five Years Ago A Was Three Times As Old As B What Are The Present Ages Of B
Answered Joey Is 20 Years Younger Than Becky In Bartleby
Ten Years Later A Will Be Twice As Old As B And Five Years Ago A Was Three Times As Old As B What Are The Present Ages Of A And
Solved 1 Tom Is Four Years Older Than Kate In Two Years Chegg Com
Sudesh Is Twice As Old As Seema If Six Years Is Subtracted From Seema S Age And Four Years Are Added To Sudesh S Age Sudesh Will Be Four Times Seema S Age How Old
Mrs Jain Is 27 Years Older Than Her Daughter Nilu After 8 Years She Will Be Twice As Old As Youtube
Five Years Ago Nuri Was Thrice As Old As Sonu Ten Years Video
In 5 Year S Time Pam Will Be Twice As Old As Sam Was Two Yea By Liz Benova
Sam Is 3 Times As Old As Her Little Sister Jenny But In 3 More Years He Will Be Twice As Old As Jenny Will Be Then Find Their Present Ages
Answered Joey Is 20 Years Younger Than Becky In Bartleby
Five Years Ago A Was Thrice As Old As B And Ten Years Later A Shall Be Twice As Old As B What Is Brainly In
Homework Question Aaron Is Three Times As Old As His Son In Ten Years Aaron Will Be Twice As Old As His Son How Old Is Aaron Quora
7 9 Age Word Problems Intermediate Algebra
Five Years Ago Lucky Would Be Thrice As Old As Lovely 10 Years Later Lucky Will Be Twiceas Old As Lovely How Old Are They Now
Sunita Is Twice As Old As Ashima If Six Years Is Subtracted From Ashima S And Four Years Added To Sunita S Age Then Sunita Wil Be Four Times Ashima S Age How Old Were
Ten Years Later A Will Be Twice As Old As B And Five Years Ago A Was Three Times As Old As B What Are The Present Ages Of A And B
A Is Twice Old As B Three Years Ago A Was Three Times As Old As B How Old Is A Now Ppsc Css Youtube
Five Years Ago Nuri Was Thrice As Old As Sonu Ten Years Video
View Question A Mother Is Four Times As Old As Her Daughter In 12 Years Time She Will Be Twice As Old As Her Daughter What Is The Age Of The Mother
Two Years Ago Salim Was Thrice As Old As His Daughter And Six Year Later He Will Be Four Years Older Than Twice Her Age How Old Are They Now Snapsolve
Mary Is Twice Older Than Her Sister In 5 Years Time She Will Be 2 Years Older Than Her Sister Find Youtube
To fill in the age trouble chart yet do no solve.
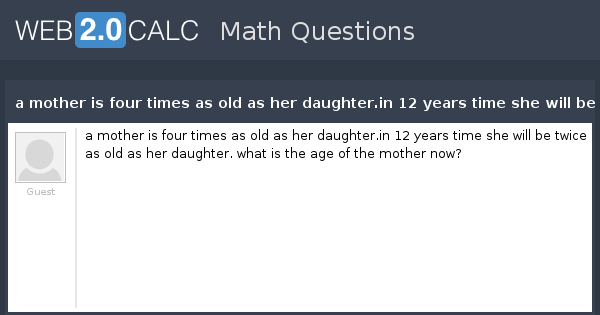
We can come up with the equation. Annes current age is 12 years. We can come up with the equation. Below you will be able to find all When asked how old she was suzie replied in two years I will be twice as old as I was five years ago How old is she. Upvote 0 Downvote. From 2 -- A 3B - 15 5 3B - 10. 1 Five years ago A was 3 times as old as B. Heres the algebraic way to figure it out. In 2 years i will be twice as old as i was 20 years ago.
James is 18 Years old Pat is 38 Years old We can write PJ20 where JAge of James and PAge of Pat In 2 years Pat will be twice as old as James or P22timesJ2 or P22J4 By putting the value in the equation We get J2022J4 or 2J-J22-4 or J18 So James is 18 Years old Therefore Pat is PJ20 or P1820 38 Years old. X age now. In two years I will be twice as old as I was five years ago. Answer 1 of 12. After two years i will be x2 years. Correct option is A Call A and B the 2 present ages. You can put this solution on YOUR website.
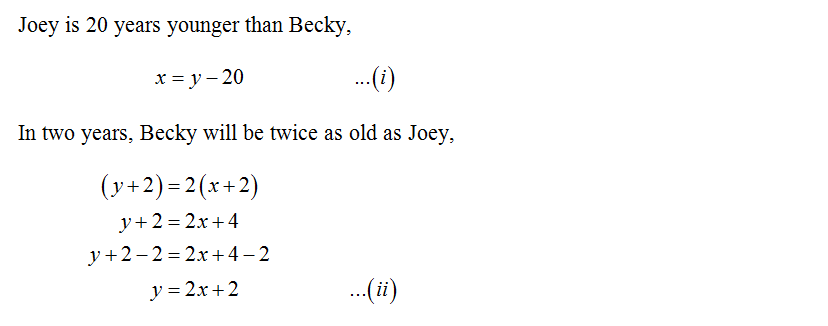
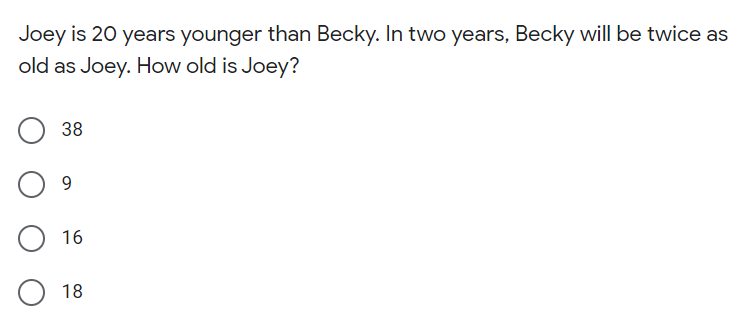
Posting Komentar untuk "In Two Years I Will Be Twice As Old"